Research

Dynamics of water on zirconia and yttria-stabilized zirconia surfaces

This project is in collaboration with the Hou’s group, in which they are investigating ZrO2 surfaces and yttria-stabilized zirconia (YSZ) surfaces on the (100), (110), and (111) crystallographic orientations in contact with an aqueous solution. We use density functional theory (DFT) calculations to obtain energetic and structural information about these systems. Additionally, to provide information on the system’s dynamics and to include temperature effects we use ab initio molecular dynamics (AIMD). Our AIMD simulations are performed at different temperatures as well as with different water surface coverages to determine the effect of chemisorbed water on the stability of the different surfaces.

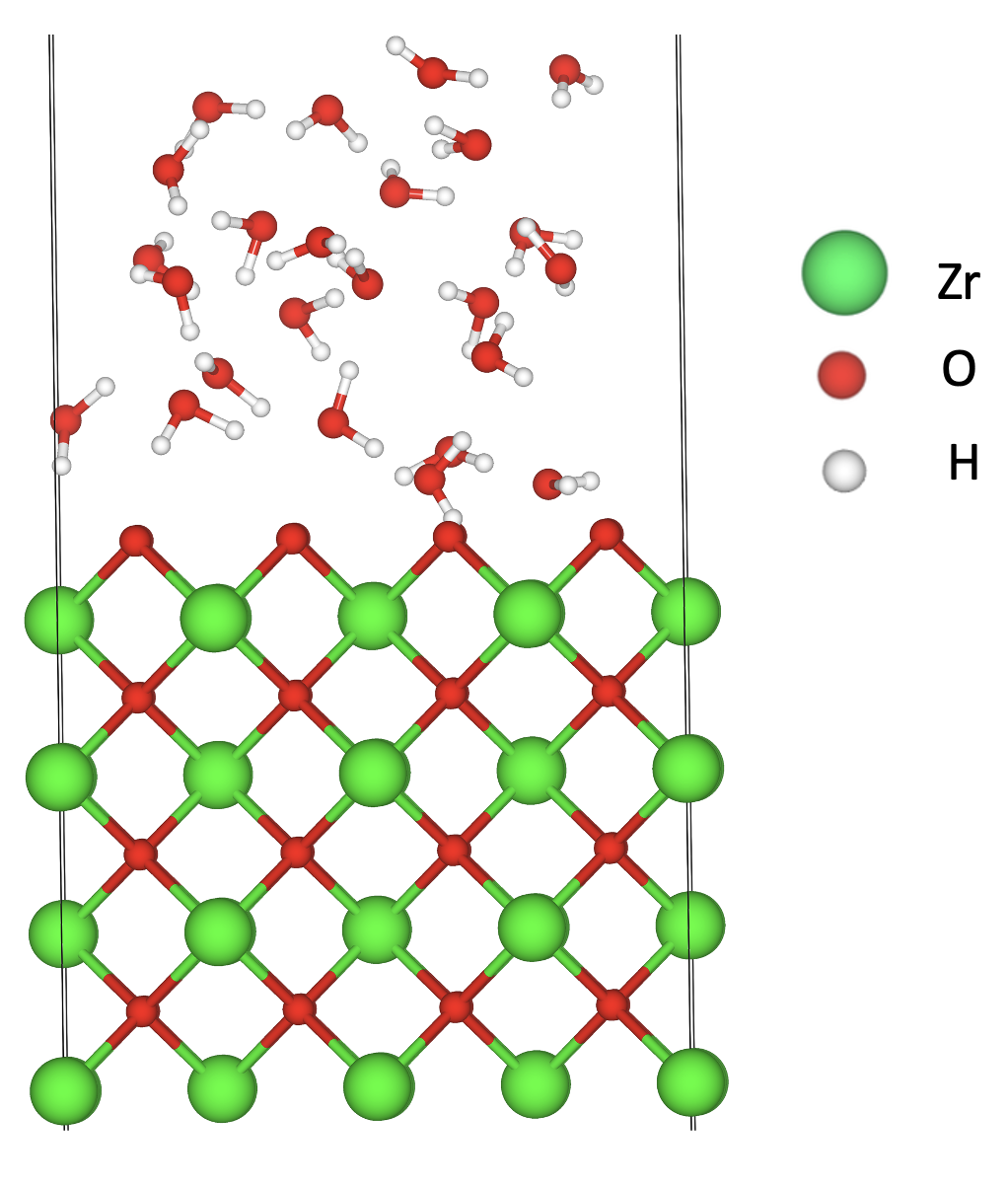
_{Molecular representation of water molecules physisorption on ZrO2(110) surface.}

Water filtration through Graphynes’ Pores

Graphyne is a carbon allotrope formed by sp and sp² carbon atoms. It is a 2D material, similar to graphene, however, it presents different types depending on the number of triple bonds connecting benzene rings. By increasing the number of triple bonds, it is possible to form pores of various sizes. Molecular dynamic (MD) studies showed that graphyne pores can be used for water purification technologies. However, their study relied on empirical force fields. To consider quantum mechanical effects we use density functional tight binding (DFTB) to describe the electronic structure of these systems. Our MD simulations are accelerated with the aid of the metadynamics (MetaD) method. 

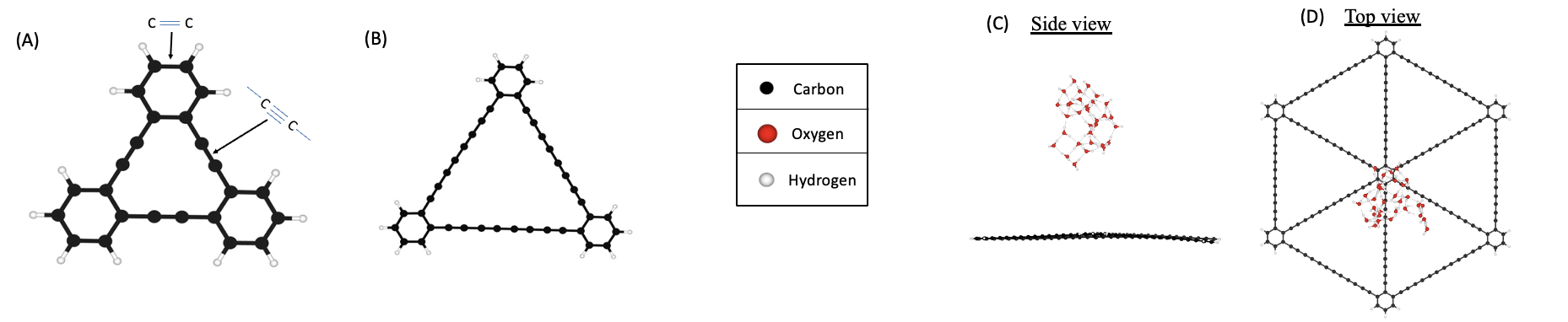
_{Molecular representation of graphyne-n units where n indicates the number of carbon-carbon triple bonds: (A) graphyne-1 (B) graphyne-4. Also shown is the setup for exploratory MetaD simulations. Side view (C) and top view (D) of a water cluster with 32 water molecules placed 10 Å away from six units of graphyne-6. The system has 300 atoms.}

Knotted protein unfolding

Knotted proteins have been identified in approximately 1% of the protein data bank entries. Knotted proteins are generally topologically more complex than unknotted proteins of similar polypeptide sequence lengths. Additionally, they have a diverse topology with different levels of complexity. Four distinct knot types have been detected in proteins: trefoil, 3₁, figure-of-eight, 4₁, three-twist, 5₂, and stevedore, 6₁, knots. In this project, we seek to better understand how the presence of a molecular knot affects a protein’s unfolding mechanism compared to a similar unknotted protein. To accomplish this we are studying the free energy surface (FES) of the unfolding/unknotting as a function of the fraction of native contacts. To overcome the high-energy barriers along the free energy surface (FES) of these proteins we use metadynamics.

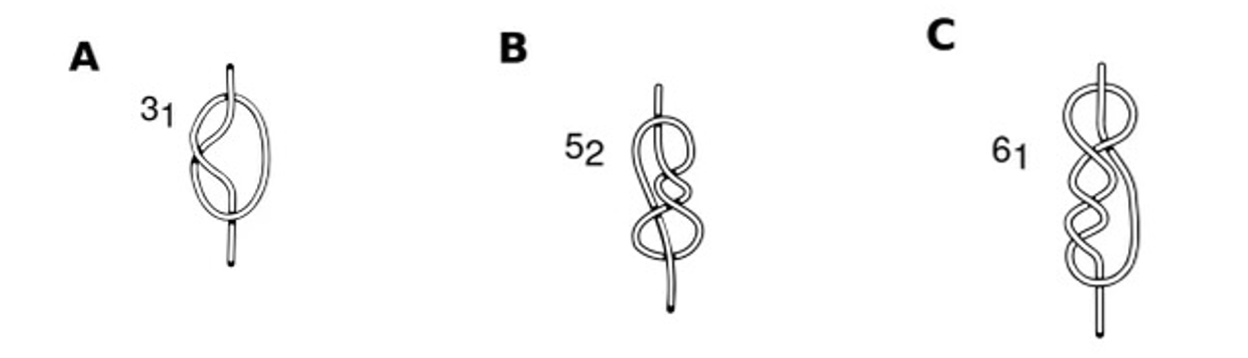
_{Schematic view of (A) 31 (B) 52 and (C) 61, knots. Figure adapted from Fonseka, Javidi, Oliveira et al. J. Phys. Chem. B 2021, 125, 27, 7335}